Pedagogia Magistério Educação Psicopedagogia Psicomotricidade, Religião, Vaishinavismo Iskcon (vulgo hinduísmo) Envie sua sugestão, crítica, dúvidas, perguntas para meu e-mail:joaomariaandarilhoutopico@gmail.com ou joaocarlosmaria@yahoo.com.br
sexta-feira, 20 de novembro de 2020
Atividades adaptadas da Avaliação da Aprendizagem em Processo (AAP) de Matemática da 1ª série do E.M de 2019 para aluna Deficiência Intelectual que se encontra na Hipóteses Silábico com valor sonoro.
quarta-feira, 18 de novembro de 2020
A Lei de Benford e a beleza dos números
Conte o número de habitantes de cada cidade brasileira. Coloque isso numa tabela e me diga, quantas vezes cada número (de 1 a 9) se repete como primeiro dígito da contagem. Tá, nós temos 5570 municípios no Brasil, contar a frequência de cada primeiro dígito vai cansar então pode chutar vai, eu deixo. Me diz qual a probabilidade de encontrar o 1 como primeiro dígito? E qual a probabilidade de encontrar o 2 como primeiro dígito?
E se eu te dissesse que, ao contrário do que imaginamos, a distribuição de “primeiros digitos” não é a mesma para os algarismos de 1 a 9 😱😱😱 Pelo menos não num conjunto “natural” ou de números aleatórios.
Os primeiros dígitos num conjunto númerico
Okay, se o que a gente esperava não é verdade, então qual é a verdadeira distribuição?! Foi essa pergunta que Frank Benford ajudou a responder.
Frank Benford
Benford era um físico americano que pegou as observações iniciais de um astronomo Simon Newcomb, generalizou e aplicou para vários datasets provando a existência de um padrão diferente daquele que a gente pensava ali no começo do post.
A Lei
Também conhecida como a Lei dos Primeiros Dígitos, a Lei de Benford define que a probabilidade do primeiro dígito de um número segue uma função logaritímica que mostro abaixo:
\[P (d) = \log_{10} \left(1 + \frac{1}{d} \right)\]A probabilidadade do primeiro dígito de um número ser \(d\) é dada pelo \(\log\) na base \(10\) de \(1 + \frac{1}{d}\). Por exemplo se tomarmos \(d = 1\) e \(d = 9\) temos:
\[P (1) = \log_{10} \left(1 + \frac{1}{1} \right) = \log_{10} \left(1+1\right) = \log_{10} 2 = 0.3010\] \[P (9) = \log_{10} \left(1 + \frac{1}{9} \right) = \log_{10} \left(1+0.11\right) = \log_{10} 1.11 = 0.0453\]Com isso sabemos que, a probabilidade de termos um \(1\) como primeiro dígito é seis vezes maior de encontrarmos um \(9\) como primeiro dígito. Louco né?
Isso é muita matemática pra mim, cadê o código?
Vamos lá! Hoje vou usar R para demonstrar com código como funciona a Lei de Benford. O objetivo dos passos a seguir é crirar um script que gere automáticamente duas coisas:
- o gráfico da análise de benford;
- o gráfico para a frequência de cada um dos primeiros dígitos no nosso dataset.
Instalando
Comece instalando o R seguindo as instruções disponíveis no site oficial do projeto.
Depois no seu diretório de trabalho, crie um arquivo para instalar as dependências, você pode chamar esse arquivo do que quiser, aqui vou chamar de install_packages.R:
options(repos = subset(getCRANmirrors(), Country == "Brazil")$URL)
install.packages("benford.analysis")
O install_packages.R se encarrega de instalar o pacote benford.analysis que traz pronto um conjunto de funções para analisar os dados contra a distribuição de Benford. Para rodar fazemos:
$ Rscript install_packages.R
Rodando o script
Depois criei um arquivo que chamei de benfords_law.R que vai conter os próximos blocos de código.
Começamos importando/carregando o nosso pacote escolhido. Depois escolhi um dataset que vem com o pacote para esse exemplo (você pode carregar o seu próprio dataset se quiser). Nosso dataset contém o censo da População das Cidades dos Estados Unidos em 2009, veja:
require("benford.analysis") # Carrega o pacote benford.analysis
data("census.2009") # Carrega o dataset
A função principal desse pacote é a benford(), é ela que faz todos os cálculos em cima dos meus dados para validá-los de acordo com a Lei de Benford. Ela irá receber um array numérico e podemos dizer quantos primeiros dígitos queremos análisar usando o argumento number.of.digits, o padrão para esse argumento é 2, mas aqui vamos usar 1 por questões demonstrativas:
bfd <- benford(census.2009$pop.2009, # Coluna com o censo por cidade em 2009
number.of.digits = 1) # Número de Primeiros Dígitos para analisar
O resultado do método benford() é uma lista. Essa lista possui oito dataframes contendo os resultados de várias contas e testes que vamos usar daqui pra frente. Algumas desses resultados são utilizados para plotar o gráfico principal da análise. E para plotar o gráfico temos o seguinte resultado:
plot(bfd)
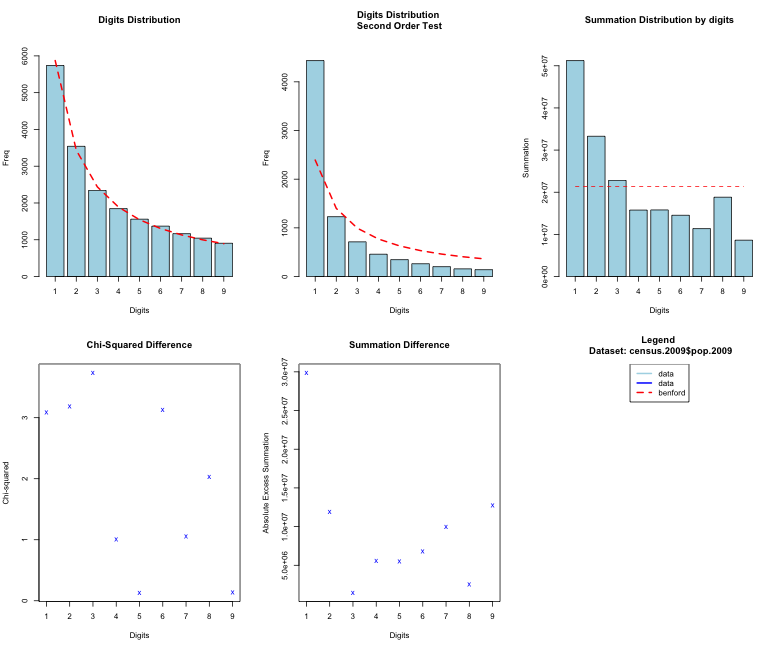
benford().Agora, vamos reproduzir o primeiro gráfico separadamente. Esse primeiro gráfico traz alguns elementos interessantes:
- Cada barra indica a frequência observada para cada primeiro dígito dentro do dataset;
- A linha vermelha traça a frequência esperada de acordo com a distribuição de Benford;
Para reproduzir esse gráfico começamos utilizando a função para plotar um gráfico de barras barplot(). Passamos para ela as frequências calculadas pela função benford() para cada primeiro dígito que se encontram em bfd$bfd$data.dist.freq. Os demais atributos setados são para deixar o gráfico de barras mais próximo do gráfico original.
barplot(bfd$bfd$data.dist.freq, # Valores de frequencia para cada barra
names.arg = bfd$bfd$digits, # Legenda de cada barra no eixo x
col = "#A1DCF0", # Coloração das barras
main = "Digits Distribution", # Título principal
xlab = "Digits", # Legenda eixo x
ylab = "Freq", # Legenda eixo y
ylim = range(0:6000), # Limite no eixo y
xlim = range(0:10), # Limite no eixo x
width = .85) # Largura da barra
Como gráficos em R são feitos por camadas, podemos adicionar a linha vermelha usando uma outra função chamada lines(). Essa função acrescenta uma nova camada em cima do gráfico plotado anteriormente criando uma linha. No gráfico original, a linha vermelha corresponde a frequência esperada de cada dígito de acordo com a distribuição de Benford e estão armazenadas em bfd$bfd$benford.dist.freq , então é só passar esse objeto para a função lines(), vejamos:
lines(x = bfd$bfd$benford.dist.freq, # Pontos para formar a linha
col = "red", # Cor da linha
lwd=2.5, # Espessura da linha
type="c") # Tipo da linha: tracejado
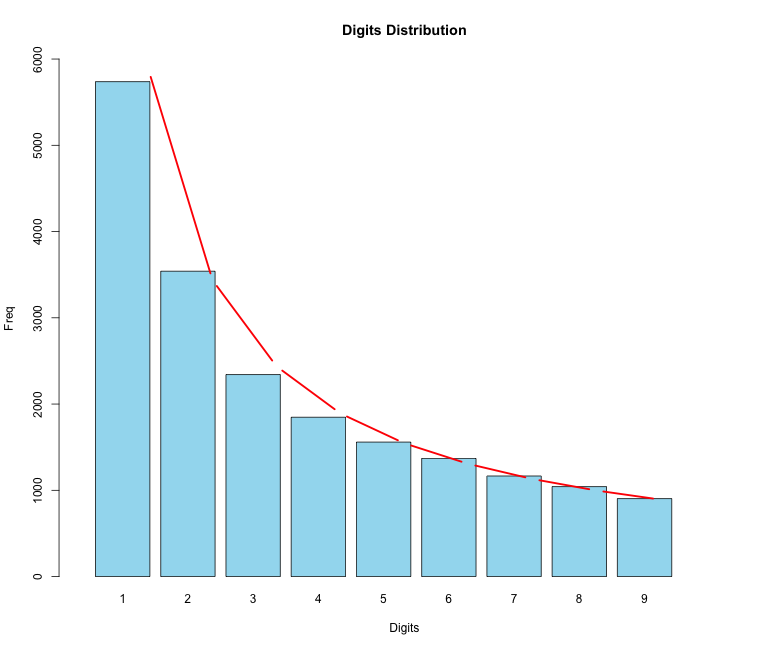
barplot().Nota com a linha vermelha quase sobrepõe o topo das barras de frequência?! Então da para perceber como o pacote benford.analysis ajuda bastante já que não é necessário fazer na mão todos esses cálculos. Esses são algumas funções básicas, você pode também realizar o teste de qui-quadrado em cima dos dados usando a distribuição de Benford e outras estatísticas.
Benford pra quê?
Tá, mas pra quê isso tudo isso é útil?
Conjuntos númericos que são “gerados naturalmente” ou que sofrem muitas transformações matemáticas como censo populacional, apuração de votações, valores de ações e estatísticas de acesso a sites, são exemplos de datasets que se aproximam da Lei de Benford.
Seres humanos tentando burlar números, muitas vezes desconhecem a Lei de Benford e assumem que os dígitos tem a mesma probabilidade de aparecer ou seguem algum outro padrão diferente do evidenciado por Benford.
Já se usou até a Lei de Benford para identificar diferenças entre frames de leitura de procariotos e eucariotos, mas seu uso mais comum é na identificação de fraudes principalmente em dataset contábeis 💰.
Leitura extra
Aqui tem uns links que andei lendo para ajudar na escrita desse post 💁
- Todos os códigos estão nesse repo do GitHub lá também tem um exemplo bem simples de como gerar “fake data” 🙊
- Blog post do Giga Matemática: Lei de Benford
- Um blogpost (em inglês) sobre como plotar a lei de Benford sem o uso da biblioteca que usei nesse post: Benford’s Law Graphed in R
- Vídeo (em inglês) sobre o uso da Lei de Benford para detecção de fraude financeira do Business Insider: How Forensic Accountants Use Benford’s Law To Detect Fraud
- Blogpost (em inglês) do DataGenetics: Benford’s Law
- Following Benford’s Law, or Looking Out for No. 1
fonte: https://jtemporal.com/benford-law/
Obrigado pela visita, volte sempre.
Conheça as nomenclaturas do Yoga
A palavra yoga vem do Sânscrito e tem diversos significados. A palavra deriva da raiz yuj, que significa “controlar”, “jungir”, ou “unir”. Algumas das traduções também incluem os significados de “juntando”, “unindo”, “união”, “conjunção” e “meios”. O praticante de yoga em nível avançado é chamado de Yogue.
O alfabeto sânscrito, devanágari, o termo é originalmente escrito desta forma: योग. Provém da raiz sânscrita yuj, que significa “jungir”, “cangar”, “arrear”, “atrelar”, “prender”, “juntar”.
A idéia de que a raiz “yuj” poderia significar “unir” no sentido de “integrar” (física ou misticamente) surge possivelmente a partir de uma afirmação vedantina que define o Yogaoga como a “união” entre o Jivatma e o Paramatma, que na verdade passam a ser um só.
Saudações ao Sol
Súrya namaskar: Súrya = Sol, namaskar = saudação; saudação ao Sol
Dentro dos súrya namaskar A e B há as seguintes posturas:
Samasthitih: sama = igual, sthitih = ficar firmemente ereto; postura equilibrada e estável
Uttanásana: uttana = alongamento intenso; postura de alongamento intenso (para a frente)
Chaturanga dandásana: chatur = quatro, anga = membros, danda = bastão; postura do bastão com apoio em quatro membros
Adhomukha svanásana: adho = para baixo, mukha = rosto, face, svana = cachorro; postura do cachorro olhando para baixo
Urdhvamukha svanásana: urdhva = para cima, mukha = rosto, face, svana = cachorro; postura do cachorro olhando para cima
Utkatásana: utka = poderoso, feroz; postura poderosa
Virabhadrásana: virabhadra = “herói virtuoso”; postura do herói Virabhadra, personificação da fúria do deus Shiva
Padangusthásana: pada = pé, angustha = dedão do pé; postura do dedão do pé
Padahastásana: pada = pé, hasta = mão; postura da mão embaixo do pé
Utthita trikonásana: utthita = estendido, tri = três, kona = ângulo; postura do triângulo estendido
Parivritta trikonásana: parivritta = torcido, tri = três, kona = ângulo; postura do triângulo torcido
Utthita parsvakonásana: utthita = estendido, parsva = lado, kona = ângulo; postura do ângulo estendido para o lado
Parivritta parsvakonásana: parivritta = torcido, parsva = lado, kona = ângulo; postura do ângulo para o lado com torção
Prasarita padottanásana: prasarita = afastado, pada = pé, uttana = alongamento intenso; postura de alongamento intenso com os pés afastados
Parsvottanásana: parsva = lado, uttana = alongamento intenso; postura de alongamento lateral intenso
Posturas de equilíbrio e de estabilidade
Utthita hasta padangusthásana: utthita = estendido, hasta = mão, angustha = dedão do pé; postura estendida com a mão no dedão do pé
Ardha baddha padmottanásana: ardha = metade, meio, baddha = entrelaçado, padma = lótus, uttana = alongamento intenso; postura do alongamento intenso com meio lótus entrelaçado
Utkatásana: utka = poderoso, feroz; postura poderosa
Virabhadrásana: virabhadra = herói; postura do herói Virabhadra
Dandásana: danda = bastão, pão; postura de estender pernas e tronco retos como um pão
Posturas sentadas e de chão
Paschimottanásana: paschima = ocidental (oeste, nesse caso, são as costas, pois se pratica ásana de frente para o leste, onde nasce o Sol; por isso, “saudação ao Sol”), uttana = alongamento intenso; postura de alongamento intenso das costas
Purvottanásana: purva = oriental (= a frente do corpo), uttana = alongamento intenso; postura do alongamento intenso da parte anterior do corpo
Ardha baddha padma paschimottanásana: ardha = metade, baddha = entrelaçado, padma = lótus, paschima = oeste (aqui, as costas), uttana = alongamento intenso; postura do alongamento intenso das costas com meio lótus entrelaçado
Triang mukhaikapada paschimottanásana: tri = três, anga = membro, mukha = face, eka = um, pada = pé, paschima = oeste (costas), uttana = alongamento intenso; postura do alongamento intenso das costas com três membros (dois braços e a cabeça/face) em direção a um pé
Janu sirsásana: janu = joelho, sirsa = cabeça; postura da cabeça em direção ao joelho
Marichyásana: Marichi = nome de um grande sábio, filho de Brahmá; postura de Marichi
Navásana: nava = barco; postura do barco
Bhujapidásana: bhuja = braço, ombro, pida = pressão; postura da pressão nos ombros
Kurmásana: kurma = tartaruga; postura da tartaruga
Supta kurmásana: supta = deitado, dormindo, kurma = tartaruga; postura da tartaruga deitada
Garbhapindásana: garbha = ventre, útero, pinda = embrião; postura do embrião no útero
Kukkutásana: kukkuta = galo; postura do galo
Baddhakonásana: baddha = entrelaçado, kona = ângulo; postura entrelaçada do ângulo
Upavishta konásana: upavishta = sentado, kona = ângulo; postura do ângulo sentado
Supta konásana: supta = deitado, dormindo, kona = ângulo; postura do ângulo deitado
Supta padangusthásana: supta = deitado, dormindo, pada = pé, angustha = dedão do pé; postura deitada (com a mão no) dedão do pé
Chakrásana: chakra = roda; postura de rodar (para trás)
Ubhaya padangusthásana: ubhaya = ambos, pada = pé, angustha = dedão do pé; postura (das mãos) em ambos os dedões dos pés
Urdhvamukha paschimottanásana: urdhva = para cima, mukha = rosto, paschima = para oeste, uttana = alongamento intenso; postura do alongamento intenso das costas com o rosto olhando para cima
Setubandhásana: setu = ponte, bandha = contração, fechamento; postura de fechar (=erguer) a ponte
Posturas finais
Urdhva dhanurásana: urdhva = elevado, para cima, dhanura = arco; postura do arco elevado
Salamba sarvangásana: salamba = apoiado, sarva = todos, anga = membro; postura de elevação de todos os membros, com apoio
Halásana: hala = arado; postura do arado
Karnapidásana: karna = orelha, pida = pressão; postura de pressionar as orelhas (com os joelhos)
Urdhva padmásana: urdhva = elevado, para cima, padma = lótus; postura do lótus elevado
Pindásana: pinda = embrião; postura do embrião
Matsyásana: matsya = peixe; postura do peixe
Uttana padásana: uttana = alongado, pada = pé, perna; postura das pernas alongadas
Sirsásana: sirsa= cabeça; parada de cabeça
Baddha padmásana (yoga mudrá): baddha = entrelaçado, padma = lótus; postura do lótus entrelaçada
Padmásana: padma = lótus; postura de lótus
Uthpluthih (também chamado tolásana): uthpluthih = elevação (tola = balança; postura da balança)
Shavásana: sava = cadáver; postura do cadáver (relaxamento final)
Nomenclatura em Sânscrito
Os nomes dos ásanas são escritos em sânscrito, uma língua antiga largamente utilizada pelas diversas linhagens da Yoga.
Adho: para baixo
Anga: partes; mebro
Angustha: dedo grande do pé
Ardha: meia; incompleta
Ayama: controle; contenção
Baddha: preso; firme; contida
Bala: criança
Banchi: bambu
Bhujanda: serpente; cobra
Bhanda: preso; montado
Bhadra: virtuoso
Chakra: roda; círculo
Chandra: lua
Chatur: quatro
Chatus: quatro
Danda: bastão
Dhanur: arco
Dola: balanço
Dvi: dois
Eka: um
Gomukha: cabeça de vaca
Hala: arado
Hasta: mão
Janur: joelho
Kona: ângulo
Karani: corpo; “um organismo que age”
Kappota: pombo
Marichya: ser mitológico ancestral do Sol
Matsya: peixe
Mukha: face; cabeça
Muktásana: liberação
Mudrá: gesto feito com as mãos
Nadi: canal; conduto
Nataraja: Shiva dançarino; o rei dos dançarinos
Nata: dança
Nava: barco
Pada: pé; perna
Padma: flor de Lotus
Pashima: parte posterior do corpo
Pavana: vento
Prana: energia vital
Pratiloma: reversão
Pristhá: costas; parte traseira de qualquer coisa
Rajas: energia
Sama: equilíbrio
Setu: ponte
Sthiti: posicionamento; estar em
Sarva: todo
Shirsha: cabeça
Shira: cabeça
Shava: cadáver
Shodana: purificação
Supta: deitado; adormecido
Svana: cachorro
Tada: montanha
Triang: três partes
Trikona: triângulo
Uttána: alongamento intenso
Urdhva: para o alto
Ushtra: camelo
Utka: cócoras
Vakra: torção
Vajrá: raio, diamante, baastão
Viparita: invertido
Vira: heroi
Yoga: união
Referências: Wikipedia, Yoga.pro, Yoga Namas
-
Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou Slideshare está com erro entre em contato.
-
Muitas pessoas com minha idade, em torno dos 40 , foram alfabetizadas com esta cartilha. Ela foi utilizada durante muitos anos. Para ver e...
-
Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou slidshre está com erro entre em contato.
-
Martinho Lutero Origem: Wikipédia, a enciclopédia livre. (Redirecionado de Martinho lutero ) Ir para: navegação , pesqu...
-
Kami Xintoísmo Origem: Wikipédia, a enciclopédia livre. Ir para: navegação , pesquisa A Wikipédia possui o Po...
-
O Vastu Shastra Vastu Shastra é a ciência da construção de casas que tragam saúde, prosperidade, paz e felicidade aos morador...
-
Escala Portage-1 from Carlos Junior Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou slidshre está com erro...
-
Data de publicação: 19/02/2000 Um homem encontrou um ovo de águia e o colocou debaixo da galinha que chocava seus ovos no quintal. Nasceu um...











