Pedagogia Magistério Educação Psicopedagogia Psicomotricidade, Religião, Vaishinavismo Iskcon (vulgo hinduísmo) Envie sua sugestão, crítica, dúvidas, perguntas para meu e-mail:joaomariaandarilhoutopico@gmail.com ou joaocarlosmaria@yahoo.com.br
sábado, 21 de novembro de 2020
Lockdown - Farsa e uso político? - Ao Vivo
sexta-feira, 20 de novembro de 2020
Atividades adaptadas da Avaliação da Aprendizagem em Processo (AAP) de Matemática da 1ª série do E.M de 2019 para aluna Deficiência Intelectual que se encontra na Hipóteses Silábico com valor sonoro.
quarta-feira, 18 de novembro de 2020
A Lei de Benford e a beleza dos números
Conte o número de habitantes de cada cidade brasileira. Coloque isso numa tabela e me diga, quantas vezes cada número (de 1 a 9) se repete como primeiro dígito da contagem. Tá, nós temos 5570 municípios no Brasil, contar a frequência de cada primeiro dígito vai cansar então pode chutar vai, eu deixo. Me diz qual a probabilidade de encontrar o 1 como primeiro dígito? E qual a probabilidade de encontrar o 2 como primeiro dígito?
E se eu te dissesse que, ao contrário do que imaginamos, a distribuição de “primeiros digitos” não é a mesma para os algarismos de 1 a 9 😱😱😱 Pelo menos não num conjunto “natural” ou de números aleatórios.
Os primeiros dígitos num conjunto númerico
Okay, se o que a gente esperava não é verdade, então qual é a verdadeira distribuição?! Foi essa pergunta que Frank Benford ajudou a responder.
Frank Benford
Benford era um físico americano que pegou as observações iniciais de um astronomo Simon Newcomb, generalizou e aplicou para vários datasets provando a existência de um padrão diferente daquele que a gente pensava ali no começo do post.
A Lei
Também conhecida como a Lei dos Primeiros Dígitos, a Lei de Benford define que a probabilidade do primeiro dígito de um número segue uma função logaritímica que mostro abaixo:
\[P (d) = \log_{10} \left(1 + \frac{1}{d} \right)\]A probabilidadade do primeiro dígito de um número ser \(d\) é dada pelo \(\log\) na base \(10\) de \(1 + \frac{1}{d}\). Por exemplo se tomarmos \(d = 1\) e \(d = 9\) temos:
\[P (1) = \log_{10} \left(1 + \frac{1}{1} \right) = \log_{10} \left(1+1\right) = \log_{10} 2 = 0.3010\] \[P (9) = \log_{10} \left(1 + \frac{1}{9} \right) = \log_{10} \left(1+0.11\right) = \log_{10} 1.11 = 0.0453\]Com isso sabemos que, a probabilidade de termos um \(1\) como primeiro dígito é seis vezes maior de encontrarmos um \(9\) como primeiro dígito. Louco né?
Isso é muita matemática pra mim, cadê o código?
Vamos lá! Hoje vou usar R para demonstrar com código como funciona a Lei de Benford. O objetivo dos passos a seguir é crirar um script que gere automáticamente duas coisas:
- o gráfico da análise de benford;
- o gráfico para a frequência de cada um dos primeiros dígitos no nosso dataset.
Instalando
Comece instalando o R seguindo as instruções disponíveis no site oficial do projeto.
Depois no seu diretório de trabalho, crie um arquivo para instalar as dependências, você pode chamar esse arquivo do que quiser, aqui vou chamar de install_packages.R:
options(repos = subset(getCRANmirrors(), Country == "Brazil")$URL)
install.packages("benford.analysis")
O install_packages.R se encarrega de instalar o pacote benford.analysis que traz pronto um conjunto de funções para analisar os dados contra a distribuição de Benford. Para rodar fazemos:
$ Rscript install_packages.R
Rodando o script
Depois criei um arquivo que chamei de benfords_law.R que vai conter os próximos blocos de código.
Começamos importando/carregando o nosso pacote escolhido. Depois escolhi um dataset que vem com o pacote para esse exemplo (você pode carregar o seu próprio dataset se quiser). Nosso dataset contém o censo da População das Cidades dos Estados Unidos em 2009, veja:
require("benford.analysis") # Carrega o pacote benford.analysis
data("census.2009") # Carrega o dataset
A função principal desse pacote é a benford(), é ela que faz todos os cálculos em cima dos meus dados para validá-los de acordo com a Lei de Benford. Ela irá receber um array numérico e podemos dizer quantos primeiros dígitos queremos análisar usando o argumento number.of.digits, o padrão para esse argumento é 2, mas aqui vamos usar 1 por questões demonstrativas:
bfd <- benford(census.2009$pop.2009, # Coluna com o censo por cidade em 2009
number.of.digits = 1) # Número de Primeiros Dígitos para analisar
O resultado do método benford() é uma lista. Essa lista possui oito dataframes contendo os resultados de várias contas e testes que vamos usar daqui pra frente. Algumas desses resultados são utilizados para plotar o gráfico principal da análise. E para plotar o gráfico temos o seguinte resultado:
plot(bfd)
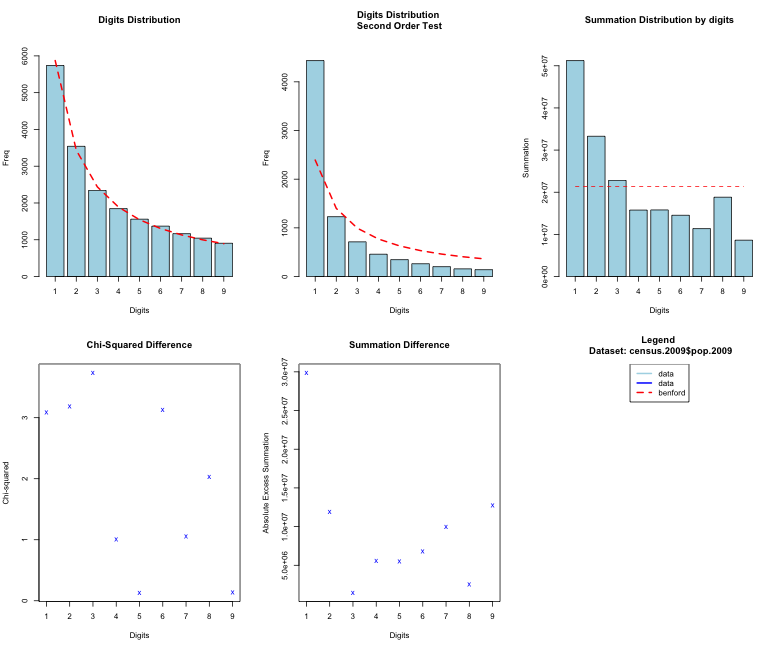
benford().Agora, vamos reproduzir o primeiro gráfico separadamente. Esse primeiro gráfico traz alguns elementos interessantes:
- Cada barra indica a frequência observada para cada primeiro dígito dentro do dataset;
- A linha vermelha traça a frequência esperada de acordo com a distribuição de Benford;
Para reproduzir esse gráfico começamos utilizando a função para plotar um gráfico de barras barplot(). Passamos para ela as frequências calculadas pela função benford() para cada primeiro dígito que se encontram em bfd$bfd$data.dist.freq. Os demais atributos setados são para deixar o gráfico de barras mais próximo do gráfico original.
barplot(bfd$bfd$data.dist.freq, # Valores de frequencia para cada barra
names.arg = bfd$bfd$digits, # Legenda de cada barra no eixo x
col = "#A1DCF0", # Coloração das barras
main = "Digits Distribution", # Título principal
xlab = "Digits", # Legenda eixo x
ylab = "Freq", # Legenda eixo y
ylim = range(0:6000), # Limite no eixo y
xlim = range(0:10), # Limite no eixo x
width = .85) # Largura da barra
Como gráficos em R são feitos por camadas, podemos adicionar a linha vermelha usando uma outra função chamada lines(). Essa função acrescenta uma nova camada em cima do gráfico plotado anteriormente criando uma linha. No gráfico original, a linha vermelha corresponde a frequência esperada de cada dígito de acordo com a distribuição de Benford e estão armazenadas em bfd$bfd$benford.dist.freq , então é só passar esse objeto para a função lines(), vejamos:
lines(x = bfd$bfd$benford.dist.freq, # Pontos para formar a linha
col = "red", # Cor da linha
lwd=2.5, # Espessura da linha
type="c") # Tipo da linha: tracejado
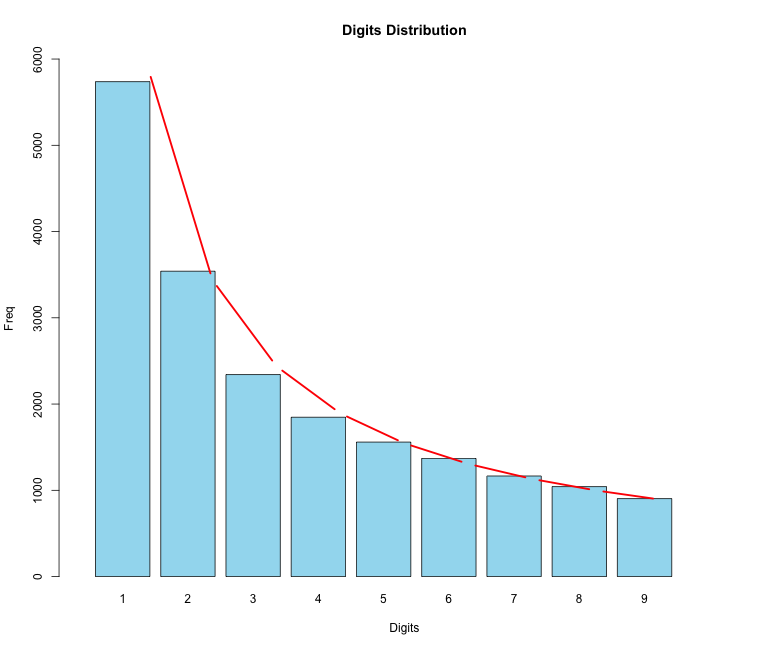
barplot().Nota com a linha vermelha quase sobrepõe o topo das barras de frequência?! Então da para perceber como o pacote benford.analysis ajuda bastante já que não é necessário fazer na mão todos esses cálculos. Esses são algumas funções básicas, você pode também realizar o teste de qui-quadrado em cima dos dados usando a distribuição de Benford e outras estatísticas.
Benford pra quê?
Tá, mas pra quê isso tudo isso é útil?
Conjuntos númericos que são “gerados naturalmente” ou que sofrem muitas transformações matemáticas como censo populacional, apuração de votações, valores de ações e estatísticas de acesso a sites, são exemplos de datasets que se aproximam da Lei de Benford.
Seres humanos tentando burlar números, muitas vezes desconhecem a Lei de Benford e assumem que os dígitos tem a mesma probabilidade de aparecer ou seguem algum outro padrão diferente do evidenciado por Benford.
Já se usou até a Lei de Benford para identificar diferenças entre frames de leitura de procariotos e eucariotos, mas seu uso mais comum é na identificação de fraudes principalmente em dataset contábeis 💰.
Leitura extra
Aqui tem uns links que andei lendo para ajudar na escrita desse post 💁
- Todos os códigos estão nesse repo do GitHub lá também tem um exemplo bem simples de como gerar “fake data” 🙊
- Blog post do Giga Matemática: Lei de Benford
- Um blogpost (em inglês) sobre como plotar a lei de Benford sem o uso da biblioteca que usei nesse post: Benford’s Law Graphed in R
- Vídeo (em inglês) sobre o uso da Lei de Benford para detecção de fraude financeira do Business Insider: How Forensic Accountants Use Benford’s Law To Detect Fraud
- Blogpost (em inglês) do DataGenetics: Benford’s Law
- Following Benford’s Law, or Looking Out for No. 1
fonte: https://jtemporal.com/benford-law/
Obrigado pela visita, volte sempre.
Como tirar parafuso quebrado - Dica Jogo Rápido
Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou Slideshare está com erro entre em contato.

-
Bhagavad-gītā 2.23 nainaṁ chindanti śastrāṇi nainaṁ dahati pāvakaḥ na cainaṁ kledayanty āpo na śoṣayati mārutaḥ Sinônimos na — nunca; e...
-
O Kali-Santarana Upanishad (sânscrito: कलिसन्तरणोपनिषद्, IAST: Kali-Saṇṭāraṇa Upaniṣad), também chamado de Kalisantaraṇopaniṣad , é u...
-
Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou slidshre está com erro entre em contato.
-
Administração De Marketing A Edição Do Novo Milênio (Philip Kotler ; tradução Bazán Tecnologia e Lingüística ; revisão técnica Arão Sapiro. ...
-
Obrigado pela visita, volte sempre. Se você observar que a postagem, vídeo ou Slideshare está com erro entre em contato.
-
Staal observa que embora o nome Yajnavalkya seja derivado de yajna , que conota ritual, Yajnavalkya é referido como "um pensador, não...
-
TDAH - Entrevista completa com Dr. Paulo Mattos - Programa do Jô - 18/08/03 Vamos entender um pouco mais deste, problema que atinge de 3 ...





.jpg)

.jpg)